小学生でも分かる不確かさの話
はじめに
最近”不確かさ”という言葉を頻繁に聞きますが、何なのでしょうか?
ネットで調べるといくらでも説明文が出てきますが、いくら読んでも結局良く分からないままではないでしょうか?
と言う訳で、ここでは小学生にも分かる様に”不確かさ”についてご説明したいと思います。
なお同じ語源(uncertainty)ですが、経済用語の”不確実性”とは全く違いますので、事前ににお伝えしておきます。
結論
答えを先に述べると、不確かさとは、本来ならば求めらない誤差を、統計処理を使って推測した値の事です。
これだけでは今一つ良く分からないと思いますますので、以下にもう少し分かり易く解説したいと思います。
誤差
それでは先ず、(説明し易いので)上記結論にあった誤差から話を進めたいと思います。
例えば鉛筆の長さを物差しで測ったら、190mm(19cm)だったとします。

この190mmを、測定値と呼びます。
ですがもし、鉛筆とスケールの端部の位置がずれていたり、スケールの先端が摩耗していたり、鉛筆とスケールが傾いていたり、更にはスケールと鉛筆の温度が異なっていたりすると、当然測定誤差を生じます。
この誤差とは測定値と真の値とのズレ量になり、以下の式で表されます。
誤差=測定値-真の値
すなわち、誤差とは測定値から真の値を引いたものです。
真の値は求められない
前述の式から、誤差を知るためには、鉛筆の本当の長さが分かれば良い事になります。
ところが、驚いた事に鉛筆の本当の長さ(真の値)は誰にも分からないのです。
実際、JIS(日本工業規格)のZ8103には、真の値を以下の様に定義しています。
真の値(true value)
ある特定の量の定義と合致する値。
備考:特別な場合を除き、観念的な値で、実際には求められない。
ある特定の量の定義と合致する値。
備考:特別な場合を除き、観念的な値で、実際には求められない。
難しく書かれていますが、これを簡単に言うと真の値とは誰にも分からないという事です。
という事は、誤差も誰にも分からないという事になってしまいます。
不確かさ
さすがにそれでは困るので、その分からない誤差を、統計処理をして推測したのが”不確かさ”というわけです。
具体的には、測定環境、測定方法、測定器、更に測定器とそれを校正した校正機と原器までの誤差の積み重ねから、ある信頼度において、真の値がどの範囲にあるかを算出します。
具体的な算出方法については、ISO(国際標準化機構)から指針が出されていますので、ここでは割愛します。
ちょっと難しくなってしまいましたが、例えばある試験所に鉛筆の長さの測定をお願いしたとすると、以下の様なデータが戻ってきます。
| 測定値 | 190mm |
| 不確かさ | ±1mm |
| 信頼度 | 95% |
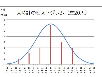
という事は、その鉛筆の真の長さは不明なものの、真の長さは189mm~191mmの範囲に95%の確立であるという事を指します。
信頼度
なんとなく不確かさが分かった所で、次に信頼度についてお話しておきましょう。
信頼度というのは、今ひとつ馴染めない言葉ですが、簡単に言うとそれがどれだけ確かそうかという事です。
例えば、あの人は信頼できる、或いは信頼できないという話は一般的に使う言葉です。
ならば、あの人は95%信頼できるとするというと、どういう意味になるでしょう?
統計的に言えば、あの人に仕事を頼むと100件中95回は期待した通りに処理してもらえるのだが、残り5%はどうなるか定かではないという事です。
ここで定かではないというのは、うまく処理されないという訳ではなく、どちらだか分からないということで、もしかしたら全て期待通りに処理される可能性もあるという事です。
この信頼度は計算でいくらでも高める事が可能ですが、弊害があります。
もし信頼度95%だと物足りないので99%にしたとしたら、計算上鉛筆の不確かさは例えば±100mmとどんどん広がってしまうことになります。
測定値が長さ190mmの鉛筆の真の長さは、99%の信頼度で90mm~290mm (9cm~29cm) の範囲の中にあると言われても、殆ど意味がありません。
と言う訳で、いたずらに信頼度を上げると、不確かさの値はどんどん広がって、却って意味のない数値になるという事を知っておいて下さい。
応用
さて、不確かさと信頼度の両方が分かった所で、この不確かさが分かるとどんな良い事があるのでしょうか。
これによって鉛筆の長さが正確に分かります、と言いたい所ですが、測定誤差の範囲を推定するだけですので実質的にはほとんどメリットはありません。
不確かさが分かる事による最大のメリットは、その測定値を全世界的に保証できる事です。
さすがに鉛筆の長さを規制している国はありませんが、例えば電子機器から発生する電磁波のノイズレベルを規制している国は多数あります。
そこに電子機器を輸出するに際して、不確かさが分かっていれば、測定誤差を考慮してもノイズレベルが規格内であるかどうかを客観的に判断できます。
例えばある周波数におけるノイズレベルの限度値が60dBで、測定値が58dBで不確かさが±2dBだとすると、真のノイズレベルは56~60dBの間にありますので、このノイズレベルはぎりぎり合格と判断できます。
ただし実際にはこれでは心配なので、もっと測定サンプル数を増やしたり、更にマージンを増やしたりして、製品の信頼性を上げる必要があります。
またもう一つのメリットはスケール側、すなわち測定する側の比較ができるという事です。
例えばA試験所とB試験所で同じ鉛筆の長さを測って貰ったら、以下の様なデータを貰ったとします。
| 内容\試験所 | A試験所 | B試験所 |
| 測定値 | 190mm | 190mm |
| 不確かさ | ±1mm | ±2mm |
| 信頼度 | 95% | 95% |
これを見るとA試験所の不確かさが±1mmで、B試験所の不確かさが±2mmですので、A試験所の方が測定精度が高いと言えます。
という訳で、不確かさは試験所あるいは測定器を校正する校正施設の測定精度を比較するのにも使えるという訳です。
なお前記しました様に、不確かさを算出するには使用する測定器の校正データが必要になりますので、それができるのは主に試験所もしくは校正施設になります。
まとめ
以上をまとめますと、以下の様になります。
①不確かさとは、誤差に代わる概念である。
②不確かさとは、信頼度という条件を付けて推定した誤差である。
③不確かさが分かれば、その測定値を世界的に保証できると共に、測定精度の比較が可能となる。
こんな説明で、少しはお役に立ちましたでしょうか?
小学生でも分かる不確かさの話