（四捨五入すると数値は大きくなる）
誰も知らなかった四捨五入の罠

1. はじめに

子供の頃から慣れ親しんできた四捨五入ですが、実は知られざる罠がある事をご存知でしょうか？


実は誰も気が付かない罠が潜んでいるのです。

今回はその罠について、じっくりご説明したいと思います。

恐らく学校の先生もご存知ないと思いますので、数字を扱う方は必見です。

問題

それでは早速問題です。

下のケースAとケースBの場合、①～③のどれが正しいと思われるでしょうか？

　　ケースA：四捨五入する前の数値を全部足してから、最後に四捨五入する。

　　ケースB：全ての数値を四捨五入して、最後にそれらを足す。

　①数値が多ければ、ケースAが大きくなる。

　②数値が多ければ、ケースBが大きくなる。

　③数値が多ければ、等しくなる。

恐らく大多数の方は、③だと思われるのではないでしょうか。

何しろ四捨五入の場合、下の表にあります様に切り捨てする場合も切り上げする場合も、同じ5個ずつなのですから。

四捨五入前	1.0	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9
四捨五入後	1	1	1	1	1	2	2	2	2	2
切り捨て/切り上げ	切り捨て					切り上げ

でも、本当にそうなるのでしょうか？

計算

という訳で、試しに計算してみましょう。

下の表は、1.0～1.9までの10個の数値をそのまま足して、後で四捨五入した場合（ケースA）と、10個の数値を事前に四捨五入してから、最後に全部を足した場合（ケースB）を表しています。

#	ケースA	ケースB
1	1.0	1
2	1.1	1
3	1.2	1
4	1.3	1
5	1.4	1
6	1.5	2
7	1.6	2
8	1.7	2
9	1.8	2
10	1.9	2
計	14.5	15
四捨五入	15

すると上の表の様に、ケースAとケースBは同じ値になりました。

何だやっぱり同じじゃないかと思われるでしょうが、ちょっとお待ち下さい。

次は、もう少しデータ数を多くしてみましょう。

データ量を多くした計算

先ほどはデータ数が1.0～1.9の10個だったので、今度は1.0～2.9までの20個で計算してみます。

#	ケースA	ケースB
1	1.0	1
2	1.1	1
3	1.2	1
4	1.3	1
5	1.4	1
6	1.5	2
7	1.6	2
8	1.7	2
9	1.8	2
10	1.9	2
11	2	2
12	2.1	2
13	2.2	2
14	2.3	2
15	2.4	2
16	2.5	3
17	2.6	3
18	2.7	3
19	2.8	3
20	2.9	3
計	39.0	40
四捨五入	39

するとどうでしょう。

何とこの場合、ケースBの方が大きくなったではありませんか。

ちなみに更に数値を多くすると、その差はもっと拡がっていきます。

そうは言っても、これは連続した数値なので、ランダムな数値だと変わってくると思う方もいらっしゃるかもしれません。

ではランダムな数値でやってみましょう。

ランダムな数値で計算

下の表は、エクセルの乱数発生関数（RAND）で作ったランダムな数値を使って求めた計算結果です。

#	ケースA	ケースB
1	8.4	8
2	0.5	1
3	6.8	7
4	3.7	4
5	3	3
6	2.2	2
7	2.7	3
8	9.5	10
9	7.8	8
10	3.3	3
11	4.4	4
12	3.6	4
13	4.6	5
14	4.8	5
15	2	2
16	1.4	1
17	9.1	9
18	3.9	4
19	4.8	5
20	0.1	0
計	86.6	88
四捨五入	87

これをご覧頂きます様に、やはりケースBの方が値が大きくなっています。

何故？

何故なのでしょう。

少し手を加えた計算

答えをお伝えする前に、下の表をご覧頂けますでしょうか。

#	ケースA	ケースB
1	8.4	8
2
3	6.8	7
4	3.7	4
5	3	3
6	2.2	2
7	2.7	3
8
9	7.8	8
10	3.3	3
11	4.4	4
12	3.6	4
13	4.6	5
14	4.8	5
15	2	2
16	1.4	1
17	9.1	9
18	3.9	4
19	4.8	5
20	0.1	0
計	76.6	77
四捨五入	77

これは先ほどのランダムな計算に、ほんの少し手を加えています。

何をしたかと言えば、（既にお気づきの様に）2番目と3番目にあった0.5と9.5を消してしまったのです。

するとケースAとケースBの値は、同じになりました。

ところが、これ以外の数値をいくら消しても、ケースBが大きいのは変わりません。

曲者は”5”

長々と話を引き延ばしてしまいましたが、ケースBの方が数値が大きくなるのは、この四捨五入する対象が”5”のときに発生するのです。

ですので、末尾に5の付いた数値が多ければ多いほど、その差は大きくなるのです。

と言う訳で、末尾が5になる数値を10個使って、同じ様な計算をしてみましょう。

#	ケースA	ケースB
1	8.5	9
2	2.5	3
3	0.5	1
4	6.5	7
5	5.5	6
6	0.5	1
7	1.5	2
8	5.5	6
9	8.5	9
10	0.5	1
計	40	45
四捨五入	40

するとご覧の様に、今まで以上にケースAとBで違いが生じています。

ここで10個の数値においては、5異なるというのを覚えておいて下さい。

理由

それでは、なぜ5を四捨五入すると、違いが生じる（大きくなる）のでしょうか？

それは（先ほどの表ではなく）、数値を目盛りで表示すると良く分かります。


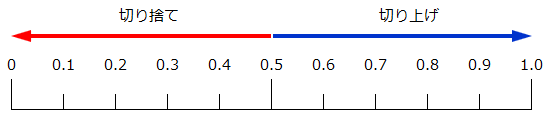
例えば小数点以下1位の数値を整数にしたい場合、ある数値が0か1のどちらか近い方の整数にします。

これを専門用語で、数値を丸める（英語でround）と呼びます。

例えば0.2であれば、0と1.0では0の方に近いので0に丸めます。

また0.7であれば、1.0の方に近いので1に丸めます。

ところが0.5の場合、0からも1.0からも同じ距離にありますので、これを丸めるとしたら0の可能性もあれば1の可能性もあるのです。

にも拘わらず、四捨五入ですと一律に1に切り上げますので、末尾が5の数値が2個以上あると必然的にその合計は四捨五入前と比べて大きくなってしまうという訳です。

ではどれだけ増えるかと言えば、末尾が5の数値が2個あると1増えるのです。

ですので、先ほど末尾が”5”となる数値が10個ある場合は、5増えたのです。

ちなみに一番最初にお見せした10個の数値の計算表でお見せした様に、末尾が”5”となる数値が1個の場合は、（当然0.5増える訳ではなく）全く増えません。

対策

それではこの問題を防ぐには、どうしたら良いでしょうか？

原因が分かれば対策は簡単です。

一つ目の対策は、個々の数値を計算する前に四捨五入しない事です。

ただし技術文書等を書くのに当たって、どうしても個々の数値を丸めなければいけない場合があります。

そんな場合は、2個ある5の一方は切り捨て、残りの5は切り上げにすれば良いのです。

JIS Z 8401 1999において、”丸めた数値として偶数倍のほうを選ぶ”としているのは、これが理由です。

JISの記述なので何を言っているか良く分からないかもしれませんが、下の表の様に例えば0.5を整数に丸め様として0と1の2種類の選択肢がある場合は、偶数である0の方を選択しろという事です。

丸める数値	丸められる選択肢		JIS推奨の方法で丸められた数値
0.5	0 or 1		0
1.5	1 or 2		2
2.5	2 or 3		2
3.5	3 or 4		4

次に、1.5を整数に丸め様として1と2の2種類の選択肢がある場合は、偶数である2の方を選択しろという事です。

なおこれは、あくまでも精度が求められる技術分野において必要なのであって、日常生活においては全く不要です。

なにしろ四捨五入するという事は、数値の精度を1桁落とす事になりますので、それに多少の誤差が生じた所で大した問題ではないからです。

ただし1個2.3円のビスを5本、5.6円のビスを7本、、、などという請求書を貰って、ビス毎に金額が整数に四捨五入されていると、余計に金額を払う事になるので、ご注意を。

まとめ

それでは最後にまとめです。

①四捨五入を行うと、数値は大きくなる。

②それは、四捨五入する対象が”5”のときに発生する。

③その理由は、５は0にも10にも同じ距離にあるため、本来ならば切り捨てと切り上げを均等に行なう必要があるからである。

④このため、正確な計算を行なうためには、四捨五入前の数値を使う必要がある。

⑤もしくは、四捨五入する対象が”5”の場合は、切り捨てと切り上げを均等に行なう必要がある。

⑥ただし日常生活においては、小学校で習った四捨五入を使って大きな問題はない。

本書がお役に立てば幸いです。