小学生でも分かる正規分布
2018/1: 発行
4. 10分でヒストグラムと正規分布カーブを描く方法
1. はじめに
お待たせしました。
小学生でも分かる正規分布の最終回です。
正規分布と標準偏差がある程度分かってくると、身近にあるデータを使って正規分布を使ってみたいとウズウズされているのではないでしょうか。
あるいは、明日のプレゼンテーションに間に合わせるために、一刻も早く正規分布のカーブを作りたい方もいらっしゃるかもしれません。
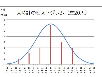
という訳でここでは、エクセルを使って、下にある(前章でお見せした)ヒストグラムとそれに対応した正規分布カーブの描き方をお伝えしたいと思います。
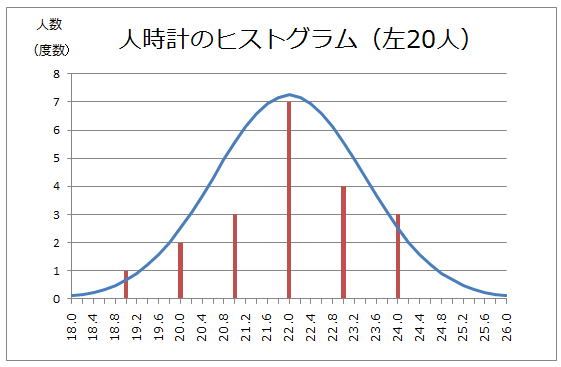
ヒストグラムとそれに対応した正規分布カーブ
エクセルの使い方さえご存じであれば、それこそものの10分で作成できますので、是非試してみて下さい。
2. 概要
それでは早速作成に取り掛かりましょう。
先ず使用するデータは、第1章で説明しました以下(左20人の人時計)のデータです。
| 表1 | |
| No. | 時間(秒) |
| 1 | 23 |
| 2 | 23 |
| 3 | 22 |
| 4 | 24 |
| 5 | 22 |
| 6 | 19 |
| 7 | 21 |
| 8 | 22 |
| 9 | 22 |
| 10 | 23 |
| 11 | 21 |
| 12 | 23 |
| 13 | 22 |
| 14 | 20 |
| 15 | 22 |
| 16 | 24 |
| 17 | 24 |
| 18 | 21 |
| 19 | 20 |
| 20 | 22 |
また正規分布で使用するエクセル関数は、NORM.DIST(データ,平均値,標準偏差,FALSE )です。
この関数の中に、これまた前章で説明しました以下の複雑な式が入っているという訳です。
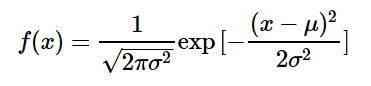
くどい様ですが、こんな難しい式は忘れて頂いて結構です。
3. 作成手順
それでは具体的な作成方法を、順を追って説明していきましょう。
①先ずエクセルを開いて、下の表1を作ります。
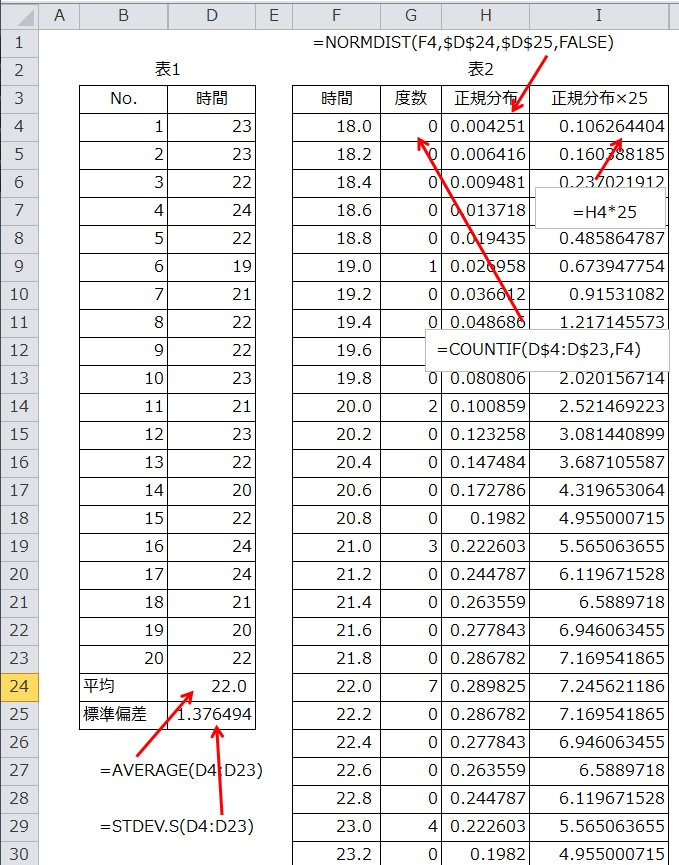
この表さえ作れば、ヒストグラムと正規分布のカーブはできたも同じ
20個のデータは前述の表をコピーするか、手入力しても2桁の数字ですので1分も掛からないでしょう。
なおこの時、入力するセルの位置が、上の表とずれたりしない様に注意してください。
またいきなり自分のデータを使うと、途中の間違いに気が付かない可能性がありますので、先ずは上と同じデータを使ってみて、本書と同じ結果になるか確認してみて下さい。
②次に20個のデータの平均値と標準偏差を求めます。
具体的には、D24とD25のセルに、下の表にある式を打ち込む(もしくはコピー&ペイスト)だけです。
| セルD24 | =AVERAGE(D4:D23) |
| セルD25 | =STDEV.S(D4:D23) |
そうすると、D24のセルに平均値の22.0が、D25のセルに標準偏差の1.376が表示されます。
③次に同じ様に表2を作って、度数(発生頻度)と正規分布の値を求めます。
具体的には、F4のセルに18.0と入力して、0.2飛びで(上の表2では23.2秒までしかありませんが)26秒まで入力します。
次にG4のセルに以下の式を入力して、オートフィルで26秒の行まで埋めます。
| セルG4 | =COUNTIF(D$4:D$23,F4) |
次にH4のセルに以下の式を入力して、オートフィルで26秒の行まで埋めます。
| セルH4 | =NORMDIST(F4,$D$24,$D$25,FALSE) |
最後にI4のセルに以下の式を入力して、同じ様にオートフィルで26秒の行まで埋めると表の完成です。
| セルI4 | =H4*25 |
なお正規分布の値(G列の値)をそのままグラフにすると、(正規分布の値は、全部足すと1にしかならない小さな値なので)値が小さくて下の横軸(X軸)に張り付いてしまいますので、ここでは度数のグラフとうまく重なる様に正規分布の値を25倍しています。
④表2が完成したら、これをグラフにします。
時間を横軸にして、度数を棒グラフ、正規分布×25を折れ線グラフにして一つのチャートにすれば、前述のヒストグラムの出来上がりです。

表2をグラフ化したチャート
簡単でしょう。
あとは表1のデータをご自分のものに変更するだけです。
ちなみにもう少しグラフの見てくれを良くしたければ、全表の時間を0.2秒間隔ではなく1秒間隔にして、カクカクした正規分布の折れ線グラフをスムージング処理すれば以下の様に多少お洒落に変更できます。
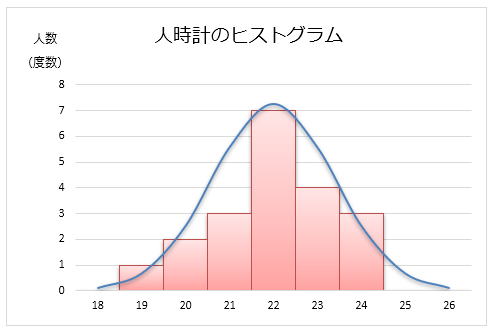
体裁を整えたヒストグラムと正規分布カーブ
ちなみに折れ線グラフをスムージングするには、①青い折れ線グラフを右クリックし、②表示された一覧から「データ系列の書式設定」をクリックし、③表示されたメニューからスムージングを選択すればOKです。
以上でチャートの描き方講座は終了なのですが、ついでに応用と捕捉事項をお伝えしておきますので、もしお時間があれば目を通しておいて下さい。
4. 応用
正規分布のグラフが完成すれば、以前紙とハサミでやった事(正規分布から不良率を求める)を、計算でも求める事ができます。
例えば19秒未満の発生率を求め様とした場合、18秒~18.8秒の正規分布である0.004251~0.019435を足すと0.0533となり、それを正規分布の総和(この場合5)で割れば1%(0.0106)となります。
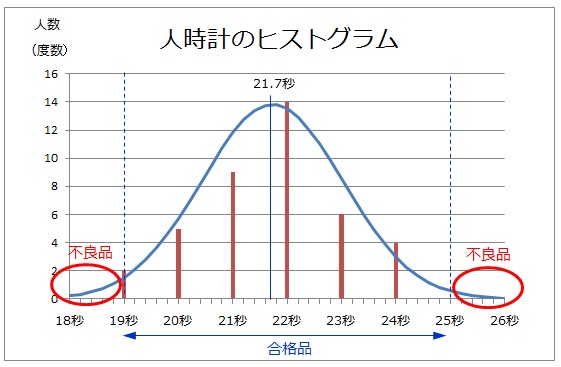
正規分布のカーブが描けたら19秒未満の発生率を求める事ができる
ところで、先程正規分布の総和は1になると言ったのに、今回の総和は5になりました。
それは正規分布のカーブを滑らかにするため横軸を5倍に広げたため、山の面積(正規分布の総和)が5倍になったためです。
ですので、発生率を求める場合、上記の様に毎回正規分布の総和を求めるのが無難です。
5. 標準偏差とサンプル標準偏差の違い
以上で終わりとしたい所ですが、最後にどうしてもお伝えしておかなければいけない事があります。
これを知っていれば、かなり自慢できます。
前項で標準偏差を求めるのに、エクセル関数のSTDEV.Sを使いましたが、これはサンプル標準偏差(もしくは標本標準偏差)と呼ばれ、今までにご説明した標準偏差(エクセルの場合、STDEV.P)とは僅かに異なります。
では何が違うのかと言えば、下にある2つの式をじっくり見比べて頂けますでしょうか。
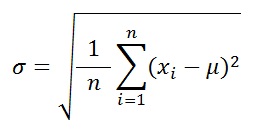
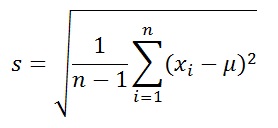
標準偏差(左) と サンプル標準偏差(右)の式
左が今までお話した標準偏差の式なのですが、これは偏差を二乗した合計をデータ数で割っていたのに対して、右のサンプル標準偏差の式はデータ数(n)から1を引いた数で割っています。
データ数を1個減らしたとなると、その背景には何かとんでもなく奥深い理由が潜んでいると思われる事でしょう。
ところがそれほど深い理由ではありません。
むしろ笑ってしまうほど簡単です。
実はサンプルで抜き取ったものから、全体像を推測する場合、通常の標準偏差を使うと実際より小さい値になります。
例えば全部で100個ある人時計の標準偏差が5だとすると、その中の10個を抜き出した場合の標準偏差は5よりも小さい値になってしまうのです。
自然界の摂理ですので、人間が考えた式と多少乖離するのは止むを得ない事かもしれません。
この補正をするために、手っ取り早くサンプル数から1を引いているのです。
早い話が現物合わせの補正をしているのです。
このため、場合によっては1ではなく、0.9や1.1の方が良いときもあるのですが、国際標準とも言えるエクセルの関数も1引いているくらいですので、一般的には1を引くのが定説と思って頂いて大丈夫です。
では1を引かない標準偏差は何に使うかといえば、全体のデータが全てある(分かっている)場合です。
通常はサンプルから全体を推測するため、現実的にはこのサンプル標準偏差しか使わないと思って頂いて構いません。
なおこの場合の記号は、σではなく、サンプル(sample)の頭文字である s を使います。
6. まとめ
これで正規分布に関する疑問点は、全て解消されましたでしょうか?
それでは最後に全体のまとめです。(①~⑤は前章からの引き継ぎです)
①正規分布とは、ある条件下で得られたバラツキのある事象の発生頻度が、左右対称の釣鐘状になる自然現象を指す。
②正規分布は自然界における多くの事象に見られる現象である。
③正規分布を知る事で、偶発的に発生する不良率や偏り、バラツキの量を知る事ができる。
④標準偏差とは、沢山あるデータ達が中心からどれくらい離れているかのバラツキ具合を示す指標である。
⑤正規分布の式は、標準偏差と平均値を使って何とか自然界の摂理とも言える正規分布のカーブを表そうと、何百年も前から多数の数学者達が研究に研究を重ねて行き着いた結果である。
⑥正規分布のカーブは、エクセル関数のNORM.DISTを使って簡単に求める事ができる。
⑤なおサンプルから全体を求める場合、標準偏差(σ)ではなくサンプル標準偏差(s)を使う。
ヒストグラムに正規分布のカーブを乗せてやれば、それだけで見栄えが良くなるだけでなく、不良率や偏りやバラツキの程度が分かりますので、是非試して頂ければと思います。
本書がお役に立てば幸いです。
4. 10分以内にヒストグラムと正規分布カーブを描く方法(4/4)