小学生でも分かる正規分布
2. 小学生でも分かる標準偏差
はじめに
ノーマルとスタンダードの違い
標準偏差の式
標準偏差の応用
まとめ
ノーマルとスタンダードの違い
標準偏差の式
標準偏差の応用
まとめ
はじめに
前章で正規分布についてご理解頂いた所で、次に標準偏差についてご説明したいと思います。
標準偏差とは、沢山あるデータ達が、中心(平均値)からどれくらい離れているかのバラツキ具合を示す指標です。
これをもう少し詳しく説明して、後は標準偏差の式の説明をすれば終わりにできるのですが、本書としてはその前にどうしてもお伝えしたい事があります。
それはノーマルとスタンダードの違いです。
それが標準偏差とどんな関係があるのかと訝(いぶか)られるかもしれませんが、今回はこの話から進めていきたいと思います。
これを知れば、標準偏差をよりスムーズに理解できます。
ノーマルとスタンダードの違い
ノーマルとスタンダードですが、実は正規分布と標準偏差の英語に使われているのです。
具体的には、正規分布がNormal Distribution、標準偏差がStandard Deviationです。
それでは何故正規分布はノーマルで、標準偏差がスタンダードなのでしょうか?
ノーマルもスタンダードも、日本では普通とか標準という意味で使われていますが、実は両者には決定的な違いがあるのです。
先ずはNormal Distributionですが、この二つの単語の意味を辞書で引くと以下の様になります。
| 英語 | 日本語 |
|---|---|
| Normal | 標準の、規定の、正規の、正常の、常態の、一般並みの、平均の、正常な発達をしている、垂直の |
| Distribution | 配分、配給、散布、分配、流通、分布、区分、分類 |
次にStandardとDeviationの単語を調べると、以下の様になります。
| 英語 | 日本語 |
|---|---|
| Standard | (比較・評価の基礎となる)標準、基準、道徳的規範、しきたり、(度量衡の)標準(器)、原器、本位、燭台、ランプ台、まっすぐな支え |
| Deviation | 逸脱、脱線、偏向、(政治信条からの)逸脱(行為)、(磁針の)自差、偏差 |
この2つ表を見比べて、本書が言いたい事に気が付いて頂けましたでしょうか?
先ずノーマルとは、人が関わらない自然界における標準だという事です。
一方、スタンダードとは、人が決めた標準だという事です。
すなわち、正規分布は自然現象だったのに対して、標準偏差は人が造ったものだという事です。
ですので正規分布の場合は、自然現象を理解すれば良かったのに対して、標準偏差は人が決めた計算方法を理解する必要があるのです。
英語圏の人ならば、Normal DistributionとStandard Deviationの間に、自然と人工の違いがある事に何となく気が付くのですが、日本語の正規分布と標準偏差にはそのニュアンスは全くありません。
ですので、(昔から言われている事ですが)理科に興味のある小学生はぜひ英語で理科の用語を覚えて頂ければと思います。
特に対数とか正規分布については、なんでこんなにも分かり難い日本語にしたのか理解に苦しみます。
と言う訳で、(前置きが非常に長くなってしまいましたが)それでは標準偏差の式を見ていきたいと思います。
式と聞いただけでうんざりされる方も多いと思いますが、人が造ったものですので、誰でも3分もあれば理解できます。
標準偏差の式
さて、その標準偏差の式は以下の通りです。
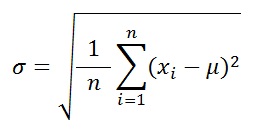
標準偏差をネットで調べると、いきなり上の式が表示されて一瞬たじろぎますが、式の意味は非常に簡単です。
と言う訳で、何故こんな式でバラツキ具合が分かるのか、これから順を追って説明していきたいと思います。
誰でも必ず理解できますので、じっくり読んでみて下さい。
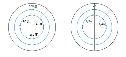
前章の人時計の比較において、右20人の方がバラツキが少ないとお伝えしましたが、その理由は中心(平均値)から離れている人が左20人より多いからです。
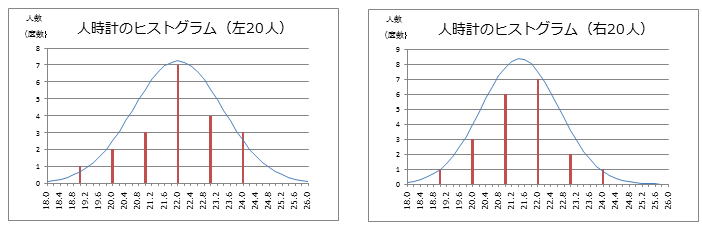
ヒストグラムだけを見比べても、どちらがバラツキが大きいか分からない
ただし上にある2枚のチャートのヒストグラム(棒グラフ)だけを見比べても、右20人と左20人のどちらがバラツキが大きいかは殆ど分かりません。
このため、バラツキの程度を正確に数値で比べるためには、一つずつのデータ(上のチャートの場合、一人一人がカウントした秒数)から中央の値(平均値)を引いて、その差を全部足せば良いと誰でも思い付くと思います。
それを式にすると以下の様になります。
バラツキ量=(各データの値-平均値)の合計
ちなみに、上記式の(各データの値-平均値)の事を偏差と呼びます。
ただしこの式のままですと、偏差の値がプラスの場合とマイナスの場合が同じ様に表れますので、それを合計するとどんどんゼロに近付いてしまいます。
それでは困るので、以下の様にマイナス分をプラスに変換するために、偏差の値を絶対値にしてやります。
バラツキ量=|各データの値-平均値|の合計
この方法でバラツキ量を計算すると、左20人が20で、右20人が19となり、右の方がバラツキが少ない事が分かります。
ただし数値を絶対値にするというのはかなり特殊な計算で、後々この式に手を加えると色々不都合が生じるため、下の式の様に絶対値の代わりに2乗する事にします。
バラツキ量=(各データの値-平均値)を2乗した合計
そうすれば数値は大きくなりますが、取り敢えずマイナスをプラスに変換できます。
この方法でバラツキ量を計算すると、左20人が36で、右20人が26.95となり、これでも右の方がバラツキが少ない事が分かります。
これで、取り敢えず右20人と左20人のバラツキ量の比較は可能なりました。
ですがもしクラスの右と左で人数が異なると、この式のままでは直接比較できなくなります。
このため、これを人数で割ってやります。
バラツキ量=(各データの値-平均値)を2乗した合計÷データ数
そうすれば、多少人数に差があってもバラツキ量を比較できます。
覚える必要は全くありませんが、これを専門用語で分散(Distribution)と呼びます。
ちなみにこの方法でバラツキ量を計算すると、左20人が1.8で、右20人が1.35となります。
そして最後にこの分散を、1/2乗し(平方根を求め)ます。
バラツキ量={(各データの値-平均値)を2乗した合計÷データ数 }^ 1/2
なぜ最後に1/2乗するかと言えば、途中で平均値との差を2乗したから、1/2乗して元に戻したというくらいに思っておいて頂ければ十分です。
この方法でバラツキ量を計算すると、左20人が1.34で、右20人が1.16となります。
そしてこのバラツキ量の式こそ、一番最初にお伝えした以下の式の意味なのです。
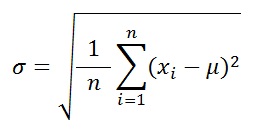
すなわち、1.34と1.16こそが、左20人と右20人の標準偏差(σ)になるのです。
どうです。びっくりする程簡単でしょう。
これで貴方は標準偏差の式の意味を、完全に理解したと言えます。
ちなみにこの式では、偏差を2乗(スクエア)して、次にそれを平均(ミーン)して、最後に平方根(ルート)を求めました。
これを、ルート・ミーン・スクエア(root mean square)と呼び、これから統計学や電気工学、品質工学を勉強するとちょくちょく目にする事になりますので、ここで覚えておきましょう。
このルート・ミーン・スクエアとは、扱うデータが、プラスとマイナスの両方になる場合の集計方法の一つ(定石)だと、覚えておけば後々役に立つと思います。
標準偏差の応用
それでは折角標準偏差の式を理解して、その値を求めたので、その応用についても簡単に触れておきたいと思います。
前述の左20人の人時計における標準偏差は1.34でした。
また左20人の人時計における平均値は、うまい具合にぴったり22です。
そして、この22から標準偏差を引いた20.66(=22-1.34)と、標準偏差を足した23.34(=22+1.34)の間が、良く耳にする±1σです。
次に、この22から標準偏差の2倍を引いた19.32(=22-2.68)と、標準偏差の2倍を足した24.68(=22+2.68)の間が±2σです。
最後に、この22から標準偏差の3倍を引いた17.98(=22-4.02)と、標準偏差の3倍を足した26.02(=22+4.02)の間が、最も良く耳にする±3σです。
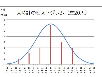
これをいつものチャートに転記すると下の様になります。
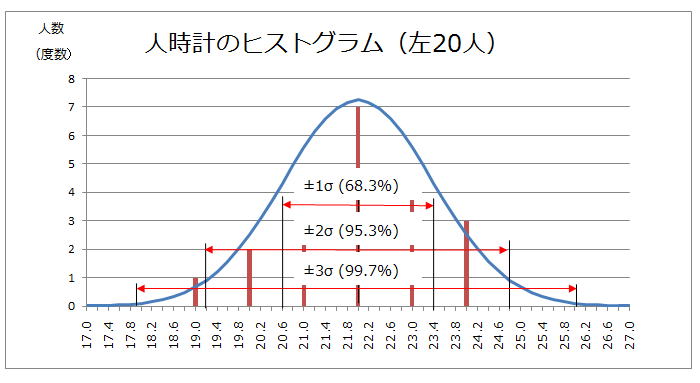
そして上のチャートにあります様に、±1σの間に挟まれる正規分布カーブの面積が全体の68.3%、±2σが95.3%、±3σが99.7%になります。
これがどういう事を表しているかと言えば、あくまでも計算上の話として、もし±3σまでを合格品だと決めたとしたら、この人時計の99.7%が良品で0.3%の不良品があるという事です。
大量に作られる工業製品は、100%良品だけにする事は不可能のため、通常この±3σを品質保証の目標にしています。
まとめ
これで標準偏差をご理解頂けましたでしょうか?
それではまとめです。
①標準偏差とは、沢山あるデータ達が、中心からどれくらい離れているかのバラツキ具合を示す指標である。
②ノーマルとは自然界の標準であり、スタンダードとは人が決めた標準である。
③理科の勉強は英語で覚えた方が分かり易い。
④ルート・ミーン・スクエア(root mean square)は大人になって役に立つ。
⑤±3σを合格だとすると、良品は全体の99.7%になる。
標準偏差の式をご理解頂いたら、次は更に難解な正規分布の式に挑戦します。
となると次をクリックする気が失せてしまうと思いますが、1分で読破できると思いますので、騙されたと思って是非覗いてみて頂ければと思います。
2. 小学生でも分かる標準偏差