小学生でも分かるデシベル(dB)の話
2. デシベルと対数
2.1. 対数について
それではここで、もう少し勉強したい方のために、デシベルの元になる対数についても簡単に勉強しておきたいと思います。
ところで、この”対数”という日本語自体が全くもって意味不明なので、対数の分かり難くさを助長している様に思います。
このため対数の英語であるロガリズム(Logarithm)を調べてみると、ギリシャ語のlogos(論理、言葉)とarithmos(数)を付けた造語という事です。
では日本ではなぜ対数と呼ぶ様になったかというと、比率を表すのに何対何という事から来た様です。
いずれにしろ、対数(これを英語に直訳するとPair Numberになります)という言葉に惑わされてはいけません。
Logarithmを勝手に分かり易く日本語に再命名すると、”桁数圧縮倍率表示法”と言った方が良いかもしれません。
話が脇道に逸れてしまいましたので、本題に戻りましょう。
先ほどのデシベルと倍率の関係を見て、ちょっとした法則に気が付いた方はいませんか?
| デシベルの差 | 倍率 |
| 0デシベル | 1倍 |
| 6デシベル | 2倍 |
| 10デシベル | 3倍 |
| 20デシベル | 10倍 |
| 40デシベル | 100倍 |
| 60デシベル | 1,000倍 |
| 80デシベル | 10,000倍 |
| 100デシベル | 100,000倍 |
| 120デシベル | 1,000,000倍 |
もし倍率の0(ゼロ)の個数とデシベルの値に何となく関係(法則)があると気が付いた方は、対数についても薄々気が付かれた事になります。
それが何かと言えば、10倍の10には0が1個あり、それが20デシベルであり、
100倍の100には0が2個あり、それが40デシベルであり、
1000倍の1000には0が3個あり、それが60デシベルになっています。
すなわち、ゼロの個数を20倍したのがデシベルになっています。
なぜ20倍するかは後で説明しますが、対数とは、上記しました”0”の個数を表しているのです。
ですので、10の対数は1で、100の対数は2で、1000の対数は3になります。
これを式で表しますと以下の様になります。
| Log10=1 | Log100=2 | Log1000=3 |
上記は分かり易い数字の場合の説明ですが、対数が何を意味するかこれでおおよそ分かって頂けたと思います。
ちなみに50の対数は1.7なのですが、これは”0”の個数が10は1個、100は2個に対して、50は1.7個(1と2の間)と考えて貰えれば良いと思います。
すなわち対数とは、数値に付く”0”の数だと覚えれば良いのです。
要は、難しい事はなるべく簡単にして理解する事です。
デシベル表示のグラフ表示
対数について分かった所で、前頁で使った以下の表をグラフ化したらどうなるか見てみたいと思います。
| 音圧レベル | 音圧(μPa) | 音の大きさ |
| 0デシベル | 20 | 人間の聴力限界 |
| 6デシベル | 40 | それより少し大きな音 |
| 10デシベル | 60 | 静かな息 |
| 20デシベル | 200 | 葉のカサカサ音 |
| 40デシベル | 2,000 | 静かな図書館 |
| 60デシベル | 20,000 | 一般的な会話 |
| 80デシベル | 200,000 | 目覚まし時計 |
| 100デシベル | 2000,000 | 地下鉄の電車 |
| 120デシベル | 20,000,000 | 飛行機の爆音 |
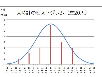
以下がそのグラフです。
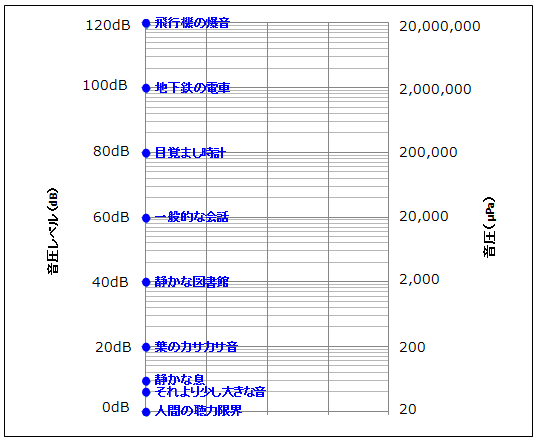
縦軸が対数表示になっていますので、各項目の間隔が均等で見易くなっています。
いきなり対数表示のグラフをお見せしましたが、対数表示のグラフとは10倍(この場合20dB)を同じ間隔にしたグラフのことです。
では、これを一般的な自然数の表示形式にしたらどうなるでしょう。
滅多に見る機会がないと思いますので、作ってみました。
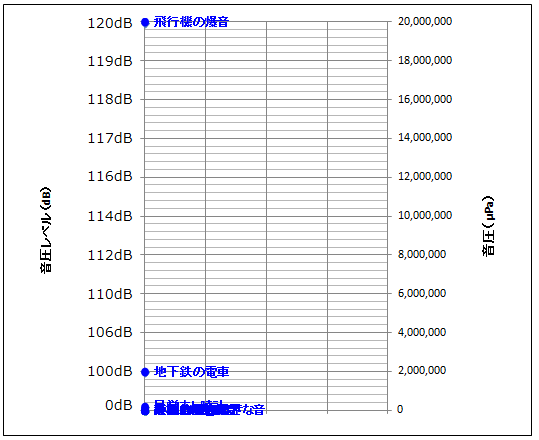
注:このグラフを見ると0dB=0μPaの様に見えますが、正確には0dB=20μPaです。
するとこんな風になってしまいます。
グラフ左の音圧レベルを見ると、0dBからいきなり100dBに上がって不自然に見えますが、グラフ右の音圧をみると、2,000,000μPaずつ均等に増えているのが分かって頂けると思います。
このグラフをご覧頂きます様に、音の大きさの様に桁数の大きな数値(桁数に意味のある数値)を普通のグラフにすると、こんなにも見難いグラフになってしまうのです。
でも中には、一番上の飛行機の爆音を抜けばもっと見易くなるのではと思われる方もいらっしゃいませんでしょうか?
ならば、飛行機の爆音を抜いてまたグラフを作ってみましょう。

するとご覧の様に、今度は地下鉄の電車が一番上に行って、他がまた最下段に集中するのは同じなのです。
対数表示の便利さを、グラフ表示でも分かって頂けたと思います。
2.2. Big Dataへの応用
突然ですが、Big Dataという言葉を聞いた事がありますでしょうか?
少々脱線しますので、もし興味が無ければ次にスキップして下さい。
元々はIT関連の言葉ですが、数値のデジタル化に伴い、身の回りのデータ量が膨大になってきました。
データ量が多くなって、その分有効な情報が多くなれば良いのですが、殆どの場合そのデータをどう処理すれば良いか分からず、結局無駄にしてしまう場合が多くあります。
そんなときに対数を使うと、今まで見えなかった様が見える様になります。
例えばですが、ある会社の月々の資産の推移が以下の表の通りだとしましょう。
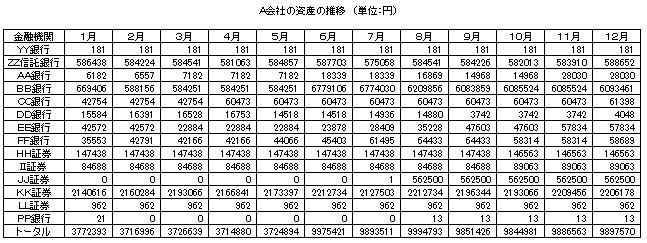
さすがにこの表を見てもと何が何だか分からないので、早速グラフにしてみました。
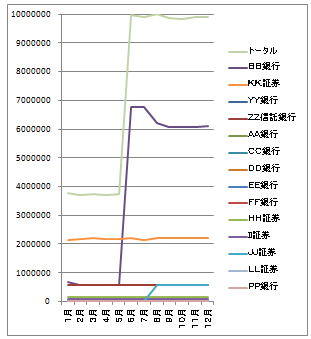
これですと、5月に資産が跳ね上がったのは分かるのですが、10万円以下の口座がどう変動しているのか全くわかりません。
ならばと高額の口座については、右側に別の単位軸を設けてみます。
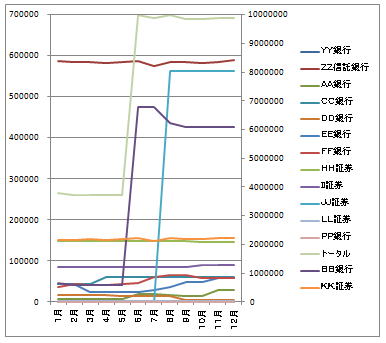
これですと、確かに少額の口座の推移は見えてきたのですが、今度は上半分にあるグラフがどちらの軸で見て良いのか分からず、却って分かりづらくなってしまいました。
恐らくこうなると、従来ならば複数のグラフに分けるしかないでしょう。
ところが、ここで対数表示を使ってみましょう。
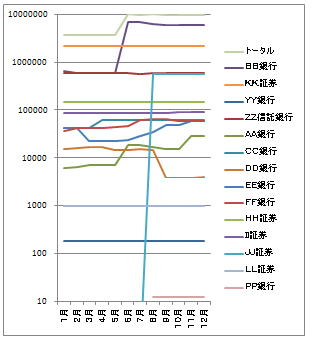
どうでしょう?
これですと下は13円から上は1千万円までが1枚のグラフに収まり、かつどの口座においても変動の傾向を把握でき、さらにそれぞれの上下関係も認識できます。
コンピュータが大衆化した事により、一昔前の手計算から人類は解放されましたが、今度はコンピュータから出力される膨大なデータを、どうやって人間が分かる様にまとめかの能力が必要になってきたという訳です。
2.3. デシベルの計算
対数の基礎が分かった所で、ここでもう少し面白い(ややこしい?)、デシベルの計算についても触れておきたいと思います。
例えばここに80デシベルの音を出す目覚まし時計が2個あります。それらが同時に鳴ったら何デシベルになるでしょうか?


80 dB + 80 dB = 160 dB?
つい80デシベルの2倍で160デシベルと答えてしまいそうですが、デシベルの計算ではそうなりません。
どうするかと言えば、前述の表において音の大きさ(倍率)が2倍になるとデシベル表示では6デシベルアップしますので、80デシベル+6デシベル=86デシベルになるという訳です。
| デシベルの差 | 倍率 |
| 0デシベル | 1倍 |
| 6デシベル | 2倍 |
| 10デシベル | 3倍 |
| 20デシベル | 10倍 |
| 40デシベル | 100倍 |
| 60デシベル | 1,000倍 |
| 80デシベル | 10,000倍 |
| 100デシベル | 100,000倍 |
| 120デシベル | 1,000,000倍 |
もしこの目覚まし時計が10個鳴ったとすると、音の大きさは10倍になりますので20デシベルアップして、100(80+20)デシベルになるという訳です。
またもし救急車2台のサイレンの音が90デシベルだったのが、もし1台になったとしたら、6デシベル(1/2)減って84(90-6)デシベルになるという訳です。

90デシベル 84デシベル
という訳で、デシベルというのは掛け算を足し算で、割り算を引き算で表すという事が何となく分かって頂けたでしょうか?
この特徴を活用して、昔(電卓が普及する前)は複雑な掛け算/割り算の計算は、対数に変換して行っていました。
それが下の計算尺です。(昔は直線型が主流だったのですが、今では製造中止になった様です)
また対数を扱う場合の注意事項として、デシベル同士の割り算、掛け算をしてはいけない事は、常識として覚えておいて下さい。
例えば、図書館の音が40デシベルで一般的な会話の音が20デシベルなので、40デシベル÷20デシベルとして両者の音の大きさが2倍違うと言うのは間違いです。
正しくは、40デシベルと20デシベルの音の大きさの差(正確には音圧の差)は20デシベルである、もしくは音の大きさ(正確には音圧)は10倍違うというのが正しい言い方です。
2.4. デシベルのマイナス表示
今まではデシベル表示は全てプラス側を述べていましたが、ここで念のためマイナス表示の場合もまとめておきましょう。
| デシベルの差 | 倍率 |
| -120デシベル | 1/1,000,000倍 |
| -100デシベル | 1/100,000倍 |
| -80デシベル | 1/10,000倍 |
| -60デシベル | 1/1,000倍 |
| -40デシベル | 1/100倍 |
| -20デシベル | 1/10倍 |
| -10デシベル | 1/3倍 |
| -6デシベル | 1/2倍 |
| 0デシベル | 1倍 |
| 6デシベル | 2倍 |
| 10デシベル | 3倍 |
| 20デシベル | 10倍 |
| 40デシベル | 100倍 |
| 60デシベル | 1,000倍 |
| 80デシベル | 10,000倍 |
| 100デシベル | 100,000倍 |
| 120デシベル | 1,000,000倍 |
上記を見て頂ければ、細かい説明は不要と思いますが、デシベルのマイナス表示は倍率が逆数になって1よりもどんどん小さくなっていくという訳です。
2.5. レベルメータのdB表示
今では殆ど見かけなくなったカセットデッキのレベルメータにも、dB表示がありました。


カセットデッキのレベルメーター
この場合の0dBとは、ここまでなら入力信号がきれいに録音できますよと設定された基準値です。
ですので、カセットテープに音楽をきれいに録音したいのでしたら、常時レベルメータの針がこの0dBを超えない(瞬間的に超える)程度に録音ボリュームを調整すれば、音割れがしないで且つノイズの少ない録音ができるという訳です。
また右上の写真では少々見難いのですが、0dBの下に100%、-5dBと-7dBの間に50%、-20dBの下に10%と表示されています。
これももう説明不要ですよね。
前段にあった以下の倍率を%に変更しているという訳です。
| レベルメーターの表示 | 倍率 | %表示 |
| -20デシベル | 1/10倍 | 10% |
| -6デシベル | 1/2倍 | 50% |
| 0デシベル | 1倍 | 100% |
またついでにお伝えしておきますと、+3dBの所にドルビーマーク(Dと逆D)が付いていますが、これはドルビー社が設定した基準レベルで磁束密度200nWb/mと決まっていますので、少なくともこのポイントは絶対値と思って良い様です。
2.6. 単位について
デシベルは倍率の表示方法ですので、本来単位付かないのですが、何を意味するのかを表すために、決め事としてdBの後に補助的に単位を付ける場合があります。
音圧のdBSPL(フォース)、電波の強さのdBm(パワー)、dBμV/m(フォース)等はその例です。
ただしこれら同士の差(或いはマージン等)を表示する場合、後半の単位(SPL、m、V/m)が消えて、またdBのみになります。
何故ならば、デシベル同士の引き算は、絶対値同士の割り算になって、単位同士も消去されるからです。
倍率には決して単位を付けてはいけません。
2.7. 本章のまとめ
本章をまとめると以下の様になります。
①対数とは、桁数を圧縮した表示方法であり、10進数に付く”0”の数を表している。
②デシベルの計算においては、掛け算を足し算で、割り算を引き算で行う。
③またデシベル同士の割り算、掛け算をしてはいけない。
④デシベルのマイナス表示は、1以下の正の数値を表す。
⑤録音レベルの0デシベルとは、ここまでなら入力信号がきれいに録音できますよと設定された基準値である。
⑥デシベルで絶対値を表示する場合は、dBの後に単位を付ける場合があるが、倍率を表す場合は単位を消す。
これでデシベルについて9割がたご理解頂いたと思うのですが、もしさらに詳しく知りたい方がありましたら、次頁をご覧下さい。
デシベル表示で誤解の多い、パワーとフォースの違いを述べています。
2. デシベルと対数/小学生でも分かるデシベル(dB)の話